19.ARIMA模型、GARCH模型

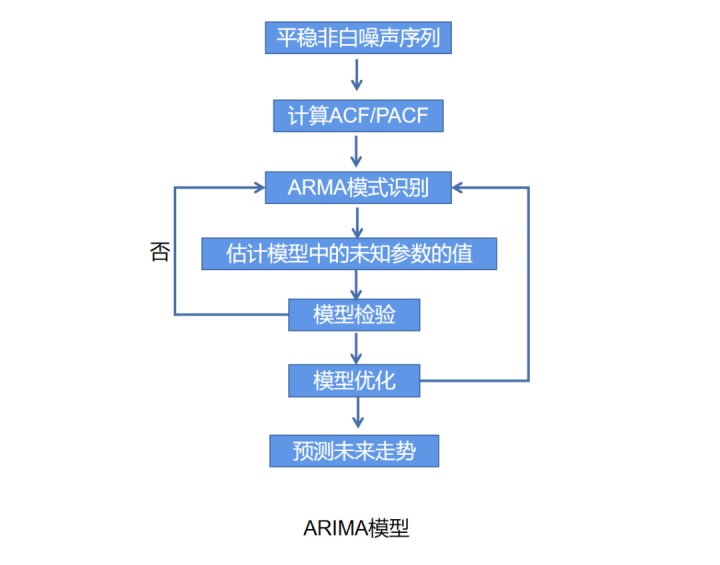
对某一个或者一组变量进行观察测量，将在一系列时刻所得到的离散数字组成的序列集合，称之为时间序列。时间序列分析是根据系统观察得到的时间序列数据，通过曲线拟合和参数估计来建立数学模型的理论和方法。时间序列分析常用于国民宏观经济控制、市场潜力预测等方面。ARIMA模型，是实际案例中最常用的模型。

20.线性规划模型

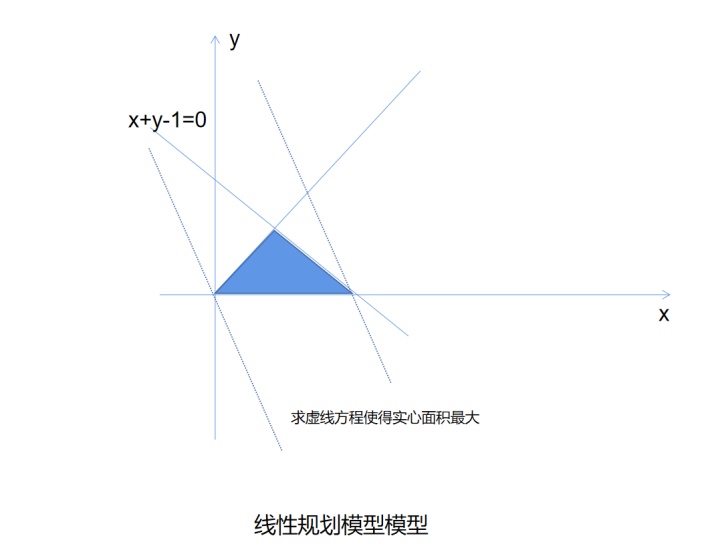
线性规划模型是指一种特殊形式的数学规划模型，即目标函数和约束条件是待求变量的线性函数、线性等式或线性不等式的数学规划模型。它所描述的典型问题是怎样以最优的方式在各项活动中间分配有限资源的问题。应用于经济分析、经营管理中，为合理地利用有限的人力、物力、财力等资源作出的最优决策。下图中是要找到最佳虚线的表达式来使得实心面积最大，约束条件就是组成实心面积的直线方程。

从实际问题中建立线性规划模型一般有以下三个步骤：1.根据影响所要达到目的的因素找到决策变量；2.由决策变量和所在达到目的之间的函数关系确定目标函数；3.由决策变量所受的限制条件确定决策变量所要满足的约束条件。